List of forcing notions
In mathematics, forcing is a method of constructing new models M[G] of set theory by adding a generic subset G of a poset P to a model M. The poset P used will determine what statements hold in the new universe (the 'extension'); to force a statement of interest thus requires construction of a suitable P. This article lists some of the posets P that have been used in this construction.
Notation
- P is a poset with order <.
- V is the universe of all sets
- M is a countable transitive model of set theory
- G is a generic subset of P over M.
Definitions
- P satisfies the countable chain condition if every antichain in P is at most countable. This implies that V and V[G] have the same cardinals (and the same cofinalities).
- A subset D of P is called dense if for every p
 P there is some q
P there is some q  D with q ≤ p.
D with q ≤ p. - A filter on P is a nonempty subset F of P such that if p < q and p
 F then q
F then q  F, and if p
F, and if p  F and q
F and q  F then there is some r
F then there is some r  F with r ≤ p and r ≤ q.
F with r ≤ p and r ≤ q. - A subset G of P is called generic over M if it is a filter that meets every dense subset of P in M.
Cohen forcing
In Cohen forcing (named after Paul Cohen) P is the set of functions from a finite subset of ω2 × ω to {0,1} and p < q if p 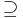 q.
q.
This poset satisfies the countable chain condition. Forcing with this poset adds ω2 distinct reals to the model; this was the poset used by Cohen in his original proof of the independence of the continuum hypothesis.
More generally, one can replace ω2 by any cardinal κ so construct a model where the continuum has size at least κ. Here, the only restriction is that κ does not have cofinality ω.
Grigorieff forcing
Grigorieff forcing (after Serge Grigorieff) destroys a free ultrafilter on ω
Hechler forcing
Hechler forcing (after Stephen Herman Hechler) is used to show that Martin's axiom implies that every family of less than c functions from ω to ω is eventually dominated by some such function.
P is the set of pairs (s,E) where s is a finite sequence of natural numbers (considered as functions from a finite ordinal to ω) and E is an element of some fixed set G of functions from ω to ω. The element (s, E) is stronger than (t,F) if t is contained in s, F is contained in E, and if k is in the domain of s but not of t then s(k)>h(k) for all h in F.
Jockusch–Soare forcing (a.k.a. forcing with 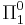 classes)
classes)
Forcing with 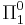 classes was invented by Robert Soare and Carl Jockusch to prove, among other results, the low basis theorem. Here P is the set of nonempty
classes was invented by Robert Soare and Carl Jockusch to prove, among other results, the low basis theorem. Here P is the set of nonempty 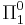 subsets of
subsets of 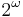 (meaning the sets of paths through infinite, computable subtrees of
(meaning the sets of paths through infinite, computable subtrees of 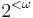 ), ordered by inclusion.
), ordered by inclusion.
Iterated forcing
Laver forcing
Laver forcing was used by Laver to show that Borel's conjecture that all strong measure zero sets are countable is consistent with ZFC. (Borel's conjecture is not consistent with the continuum hypothesis.)
- P is the set of Laver trees, ordered by inclusion.
A Laver tree p is a subset of the finite sequences of natural numbers such that
- p is a tree: p contains any initial sequence of any element of p
- p has a stem: a maximal node s(p) = s
 p such that s
p such that s 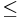 t or t
t or t 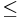 s for all t in p,
s for all t in p, - If t
 p and s
p and s 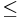 t then t has an infinite number of immediate successors tn in p for n
t then t has an infinite number of immediate successors tn in p for n  ω.
ω.
If G is generic for (P,≤), then the real {s(p) : p  G}, called a Laver-real, uniquely determines G.
G}, called a Laver-real, uniquely determines G.
Levy collapsing
These posets will collapse various cardinals, in other words force them to be equal in size to smaller cardinals.
- Collapsing a cardinal to ω: P is the set of all finite sequences of ordinals less than a given cardinal λ. If λ is uncountable then forcing with this poset collapses λ to ω.
- Collapsing a cardinal to another: P is the set of all functions from a subset of κ of cardinality less than κ to λ (for fixed cardinals κ and λ). Forcing with this poset collapses λ down to κ.
- Levy collapsing: If κ is regular and λ is inaccessible, then P is the set of functions p on subsets of λ× κ with domain of size less than κ and p(α,ξ)<α for every (α,ξ) in the domain of p. This poset collapses all cardinals less than λ onto κ, but keeps λ as the successor to κ.
Levy collapsing is named for Azriel Levy.
Magidor forcing
Amongst many forcing notions developed by Magidor, one of the best known is a generalization of Prikry forcing used to change the cofinality of a cardinal to a given smaller regular cardinal.
Mathias forcing
- An element of P is a pair consisting of a finite set s of natural numbers and an infinite set A of natural numbers such that every element of s is less than every element of A. The order is defined by (s, A) < (t,B) if t is an initial segment of s, A is a subset of B, and s is contained in t
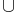 B.
B.
Mathias forcing is named for Adrian Richard David Mathias.
Namba forcing
Namba forcing (after Kanji Namba) is used to change the cofinality of ω2 to ω without collapsing ω1.
- P is the set of perfect trees in the set of finite sequences of ordinals less than ω2. P is ordered by inclusion.
Prikry forcing
In Prikry forcing (after Karel Prikry) P is the set of pairs (s,A) where s is a finite subset of a fixed measurable cardinal κ, and A is an element of a fixed normal measure D on κ. A condition (s,A) is stronger than (t, B) if t is an initial segment of s, A is contained in B, and s is contained in t 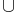 B. This forcing notion can be used to change to cofinality of κ while preserving all cardinals.
B. This forcing notion can be used to change to cofinality of κ while preserving all cardinals.
Product forcing
Taking a product of forcing conditions is a way of simultaneously forcing all the conditions.
- Finite products: If P and Q are posets, the product poset P× Q has the partial order defined by (p1, q1) ≤ (p2, q2) if p1 ≤ p2 and q1 ≤ q2.
- Infinite products: The product of a set of posets Pi, i
 I, each with a largest element 1 is the set of functions p on I with p(i)
I, each with a largest element 1 is the set of functions p on I with p(i)  P(i) and such that p(i) = 1 for all but a finite number of i. The order is given by p ≤ q if p(i) ≤ q(i) for all i.
P(i) and such that p(i) = 1 for all but a finite number of i. The order is given by p ≤ q if p(i) ≤ q(i) for all i. - The Easton product (after William Bigelow Easton) of a set of posets Pi, i
 I, where I is a set of cardinals is the set of functions p on I with p(i)
I, where I is a set of cardinals is the set of functions p on I with p(i)  P(i) and such that for every regular cardinal γ the number of elements α of γ with p(α) ≠ 1 is less than γ.
P(i) and such that for every regular cardinal γ the number of elements α of γ with p(α) ≠ 1 is less than γ.
Radin forcing
Radin forcing (after Lon Berk Radin), a technically involved generalization of Magidor forcing, adds a closed, unbounded subset to some regular cardinal λ.
If λ is a sufficiently large cardinal, then the forcing keeps λ regular, measurable, supercompact, etc.
Random forcing
- P is the set of Borel subsets of [0,1] of positive measure, where p is called stronger than q if it is contained in q. The generic set G then encodes a "random real": the unique real xG in all rational intervals [r,s]V[G] such that [r,s]V is in G. This real is "random" in the sense that if X is any subset of [0,1]V of measure 1, lying in V, then xG ∈ X.
Sacks forcing
- P is the set of all perfect trees contained in the set of finite {0,1} sequences. (A tree T is a set of finite sequences containing all initial segments of its members, and is called perfect if for any element t of T there is a tree s containing it so that both s0 and s1 are in T.) A tree p is stronger than q if p is contained in q. Forcing with perfect trees was used by Gerald Enoch Sacks to produce a real a with minimal degree of constructibility.
Shooting a fast club
For S a stationary subset of 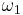 we set
we set 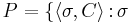 is a closed sequence from S and C is a closed unbounded subset of
is a closed sequence from S and C is a closed unbounded subset of 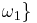 , ordered by
, ordered by 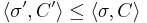 iff
iff 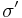 end-extends
end-extends  and
and 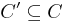 and
and 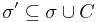 . In
. In ![V[G]](/2012-wikipedia_en_all_nopic_01_2012/I/328542dd02543fd0fd186ba17d8e11d2.png) , we have that
, we have that 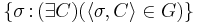 is a closed unbounded subset of S almost contained in each club set in V.
is a closed unbounded subset of S almost contained in each club set in V.  is preserved.
is preserved.
Shooting a club with countable conditions
For S a stationary subset of 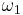 we set P equal to the set of closed countable sequences from S. In
we set P equal to the set of closed countable sequences from S. In ![V[G]](/2012-wikipedia_en_all_nopic_01_2012/I/328542dd02543fd0fd186ba17d8e11d2.png) , we have that
, we have that 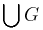 is a closed unbounded subset of S and
is a closed unbounded subset of S and 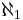 is preserved, and if CH holds then all cardinals are preserved.
is preserved, and if CH holds then all cardinals are preserved.
Shooting a club with finite conditions
For S a stationary subset of 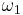 we set P equal to the set of finite sets of pairs of countable ordinals, such that if
we set P equal to the set of finite sets of pairs of countable ordinals, such that if 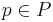 and
and 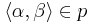 then
then 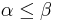 and
and 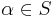 , and whenever
, and whenever 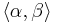 and
and 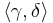 are distinct elements of p then either
are distinct elements of p then either 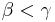 or
or 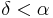 . P is ordered by reverse inclusion. In
. P is ordered by reverse inclusion. In ![V[G]](/2012-wikipedia_en_all_nopic_01_2012/I/328542dd02543fd0fd186ba17d8e11d2.png) , we have that
, we have that 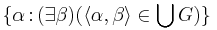 is a closed unbounded subset of S and all cardinals are preserved.
is a closed unbounded subset of S and all cardinals are preserved.
Silver forcing
Silver forcin (after Jack Howard Silver) satisfies Fusion, the Sacks property, and is minimal.
References
- Jech, Thomas (2003), Set Theory: Millennium Edition, Springer Monographs in Mathematics, Berlin, New York: Springer-Verlag, ISBN 978-3-540-44085-7
- Kunen, Kenneth (1980), Set Theory: An Introduction to Independence Proofs, Elsevier, ISBN 978-0-444-86839-8
External links
- A.Miller (2009), Forcing Tidbits.